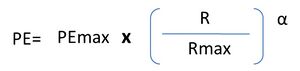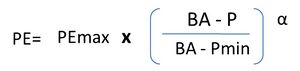Differenze tra le versioni di "Concava alla Migliore Offerta Interdipendente"
m |
|||
| (8 versioni intermedie di un altro utente non mostrate) | |||
| Riga 1: | Riga 1: | ||
[[Category:Mepa]][[Category:SDA]][[Category:AltriBandi]] | |||
Le '''Linee guida [[ANAC]] n.2,''' di attuazione del D. Lgs n.50/2016, recanti '''Offerta economicamente più vantaggiosa''' descrivono '''la formula Concava alla Migliore Offerta Interdipendente.''' | |||
* Con '''a≠1''' (non lineare). | La '''formula''' è applicabile in due forme: | ||
** per valori di α compresi tra 0 e 1 (estremi esclusi), la formula fornisce curve concave verso il basso, scoraggiando i ribassi più elevati; | * Con '''a≠1''' (''non lineare''). In base all'obiettivo è necessario scegliere il coefficiente α: | ||
** per valori di α > 1 la formula fornisce curve concave verso l’alto (o convesse), premiando i ribassi più alti e creando maggiore concorrenza sul prezzo. | ** per '''valori di α compresi tra 0 e 1''' (''estremi esclusi''), la formula fornisce curve concave verso il basso, scoraggiando i ribassi più elevati; | ||
* Con '''α=1''' (lineare) | ** per '''valori di α > 1''' la formula fornisce curve concave verso l’alto (''o convesse''), premiando i ribassi più alti e creando maggiore concorrenza sul prezzo. | ||
* Con '''α=1''' (''lineare'') la formula diventa una ''lineare''. | |||
I punteggi sono attribuiti mediante il | I punteggi sono attribuiti mediante il '''metodo dell’interpolazione lineare''' tra la '''migliore Offerta presentata''' (''cui è attribuito il punteggio massimo'') e la '''peggiore Offerta ammissibile''' (''cui è attribuito punteggio pari a zero''). | ||
La formula attribuisce '''punteggi proporzionali ai ribassi offerti rispetto alla base d’asta''', con coefficiente di proporzionalità tanto maggiore quanto minore è il massimo ribasso offerto in Gara. | |||
La formula garantisce alta '''competizione sul prezzo''', in quanto genera elevate differenze tra i punteggi attribuiti ai prezzi offerti, soprattutto nei casi in cui il miglior prezzo offerto è di poco inferiore alla base d’asta. | |||
==Formula Matematica== | |||
<div class="BloccoOrizzontale"> | |||
[[File:Formule - Concava alla Migliore Offerta Interdipendente al Ribasso.jpg|miniatura|destra|Concava alla Migliore Offerta Interdipendente al Ribasso]] | |||
'''Al Rialzo''' (''in funzione del Ribasso'')</div> | |||
<div class="BloccoOrizzontale"> | |||
[[File:Formule - Concava alla Migliore Offerta Interdipendente in Funzione del Prezzo.jpg|miniatura|destra|Concava alla Migliore Offerta Interdipendente in Funzione del Prezzo]] | |||
'''Al Ribasso''' (''in funzione del prezzo'')</div> | |||
Con: | |||
*'''PEmax''': massimo punteggio attribuibile | |||
*'''BA''': prezzo a base d’asta (''valore soglia'') [''solo in caso di formula espressa in funzione di P''] | |||
*'''R [P]''': Ribasso rispetto alla base d’asta ''(soglia)'' / prezzo (''valore'') offerto dal concorrente | |||
*'''Rmax [Pmin]''': Ribasso più elevato [''prezzo più basso''] tra quelli offerti in Gara | |||
*'''α''': esponente che regola il grado di concavità della curva | |||
Versione attuale delle 14:45, 19 ott 2023
Le Linee guida ANAC n.2, di attuazione del D. Lgs n.50/2016, recanti Offerta economicamente più vantaggiosa descrivono la formula Concava alla Migliore Offerta Interdipendente.
La formula è applicabile in due forme:
- Con a≠1 (non lineare). In base all'obiettivo è necessario scegliere il coefficiente α:
- per valori di α compresi tra 0 e 1 (estremi esclusi), la formula fornisce curve concave verso il basso, scoraggiando i ribassi più elevati;
- per valori di α > 1 la formula fornisce curve concave verso l’alto (o convesse), premiando i ribassi più alti e creando maggiore concorrenza sul prezzo.
- Con α=1 (lineare) la formula diventa una lineare.
I punteggi sono attribuiti mediante il metodo dell’interpolazione lineare tra la migliore Offerta presentata (cui è attribuito il punteggio massimo) e la peggiore Offerta ammissibile (cui è attribuito punteggio pari a zero).
La formula attribuisce punteggi proporzionali ai ribassi offerti rispetto alla base d’asta, con coefficiente di proporzionalità tanto maggiore quanto minore è il massimo ribasso offerto in Gara.
La formula garantisce alta competizione sul prezzo, in quanto genera elevate differenze tra i punteggi attribuiti ai prezzi offerti, soprattutto nei casi in cui il miglior prezzo offerto è di poco inferiore alla base d’asta.
Formula Matematica
Con:
- PEmax: massimo punteggio attribuibile
- BA: prezzo a base d’asta (valore soglia) [solo in caso di formula espressa in funzione di P]
- R [P]: Ribasso rispetto alla base d’asta (soglia) / prezzo (valore) offerto dal concorrente
- Rmax [Pmin]: Ribasso più elevato [prezzo più basso] tra quelli offerti in Gara
- α: esponente che regola il grado di concavità della curva